[백준] 2580번 : 스도쿠 (백트래킹 골드Ⅳ) - Python

문제

https://www.acmicpc.net/problem/2580

2580번: 스도쿠

문제

스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루어진 정사각형 판 위에서 이뤄지는데, 게임 시작 전 일부 칸에는 1부터 9까지의 숫자 중 하나가 쓰여 있다.

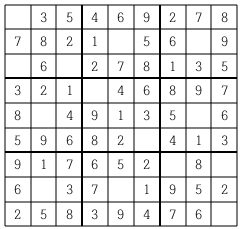
나머지 빈 칸을 채우는 방식은 다음과 같다.

1. 각각의 가로줄과 세로줄에는 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
2. 굵은 선으로 구분되어 있는 3x3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.

위의 예의 경우, 첫째 줄에는 1을 제외한 나머지 2부터 9까지의 숫자들이 이미 나타나 있으므로 첫째 줄 빈칸에는 1이 들어가야 한다.

또한 위쪽 가운데 위치한 3x3 정사각형의 경우에는 3을 제외한 나머지 숫자들이 이미 쓰여있으므로 가운데 빈 칸에는 3이 들어가야 한다.

이와 같이 빈 칸을 차례로 채워 가면 다음과 같은 최종 결과를 얻을 수 있다.

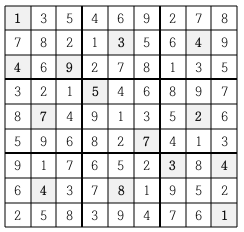
게임 시작 전 스도쿠 판에 쓰여 있는 숫자들의 정보가 주어질 때 모든 빈 칸이 채워진 최종 모습을 출력하는 프로그램을 작성하시오.

입력

아홉 줄에 걸쳐 한 줄에 9개씩 게임 시작 전 스도쿠판 각 줄에 쓰여 있는 숫자가 한 칸씩 띄워서 차례로 주어진다. 스도쿠 판의 빈 칸의 경우에는 0이 주어진다. 스도쿠 판을 규칙대로 채울 수 없는 경우의 입력은 주어지지 않는다.

출력

모든 빈 칸이 채워진 스도쿠 판의 최종 모습을 아홉 줄에 걸쳐 한 줄에 9개씩 한 칸씩 띄워서 출력한다.

스도쿠 판을 채우는 방법이 여럿인 경우는 그 중 하나만을 출력한다.

예제입력1

0 3 5 4 6 9 2 7 8
7 8 2 1 0 5 6 0 9
0 6 0 2 7 8 1 3 5
3 2 1 0 4 6 8 9 7
8 0 4 9 1 3 5 0 6
5 9 6 8 2 0 4 1 3
9 1 7 6 5 2 0 8 0
6 0 3 7 0 1 9 5 2
2 5 8 3 9 4 7 6 0

예제출력1

1 3 5 4 6 9 2 7 8
7 8 2 1 3 5 6 4 9
4 6 9 2 7 8 1 3 5
3 2 1 5 4 6 8 9 7
8 7 4 9 1 3 5 2 6
5 9 6 8 2 7 4 1 3
9 1 7 6 5 2 3 8 4
6 4 3 7 8 1 9 5 2
2 5 8 3 9 4 7 6 1

접근

이 문제는 두 가지 방법으로 풀었다.

제대로 숫자를 넣었는지 여부를 가로,세로,3X3영역으로 판단하는 것은 같지만,

백트래킹을 사용하는 방법, 즉 종료 조건이 다르다.

1. 숫자를 차례대로 넣어가며 넣을 때 마다 가로,세로,3X3영역을 체크하는 방법 (모든 빈칸에 대해 백트래킹 수행)
   • 빈 칸의 갯수대로 DFS를 다 수행했다면 완료로 처리한다.
2. 숫자의 총 합을 사용해 전체 빈칸을 제대로 채웠는지 확인하는 방법
   • 모든 셀의 합이 405라면 완료로 처리한다.

첫 번째 방법

가로줄, 세로줄, 그리고 3X3 영역 안의 숫자들을 체크해 해당 칸에 들어갈 수 있는 후보들을 추리고,

빈칸에 들어갈 수 있는 여러 경우를 조합해보며 답을 찾는 것이다.

하지만 이를 코드로 구현하려면 후보를 추릴 때 이미 한번씩 넣어봐야 하므로, 추린 후에 또 넣어보며 체크하는 것은 낭비이다.

1. 그래서 각 조건에 따라 탐색하고, 
   1. 가로줄
   2. 세로줄
   3. 3X3 영역
2. DFS를 사용해 재귀적으로 탐색
3. 가능한 답이 나오면 종료하고 반환한다. (스도쿠 판을 채우는 방법이 여럿인 경우는 그 중 하나만을 출력하라고 했으므로)

두 번째 방법

1. 첫번째와 마찬가지로 빈칸을 각 조건에 따라 탐색한다.
   • 행, 열, 3x3 영역
2. 총 합이 405가 아닌 경우 재귀적으로 탐색
3. 합이 405가 되면 종료 후 반환

첫번째 방법

풀이과정

1. 초기 조건

우선은 입력에 따라 스도쿠 판과 빈칸 정보를 완성해줘야 한다.

스도쿠 판은 9X9라고 주어졌으므로, 많이 사용될 것 같아 상수로 뽑아줬다.

import sys

SIZE = 9

# 스도쿠 문제
sudoku = [list(map(int,sys.stdin.readline().split())) for _ in range(SIZE)] 

# 빈칸의 좌표를 나타낸 리스트
blank_coord = [(i, j) for i in range(SIZE) for j in range(SIZE) if sudoku[i][j] == 0]

참고로 빈칸의 좌표를 뽑게 되면

[[0, 0], [1, 4], [1, 7], [2, 0], [2, 2], [3, 3], [4, 1], [4, 7], 
[5, 5], [6, 6], [6, 8], [7, 1], [7, 4], [8, 8]]

의 이차원 배열 형태로 나타나게 되는데, 여기서 [1,4]는 이차원 리스트의 좌표이다.

즉 1행의 4열이므로, 1을 y좌표(행, 세로로 몇 번째), 4를 x좌표(열, 가로로 몇 번째)로 정했다.

따라서 빈칸과 스도쿠 판 모두 [y, x] 인덱스의 형태를 가진다.

2. 각 조건 체크

행 체크, 즉 같은 열의 다른 행에 넣으려는 수가 이미 있는지

def check_column(x, check_num):
    for i in range(SIZE):
        if check_num == sudoku[i][x]: # 해당 수가 이미 있다면
            return False # False를 반환해 돌아간다.
    return True

열 체크, 즉 같은 행의 다른 열에 넣으려는 수가 이미 있는지

def check_row(y, check_num):
    for i in range(SIZE):
        if check_num == sudoku[y][i]:  # 해당 수가 이미 있다면
            return False # False를 반환해 돌아간다.
    return True

넣으려는 수가 3X3 영역에 이미 있는지

def check_square(y, x, n):

    BOX_SIZE = 3 # 3X3영역이므로
    
    for i in range(BOX_SIZE):
        for j in range(BOX_SIZE):
             # 해당 수가 이미 있다면
            if check_num == sudoku[y//BOX_SIZE * BOX_SIZE + i][x//BOX_SIZE * BOX_SIZE + j]:
                return False # False를 반환해 돌아간다.
    return True

그리고 이걸 굳이 세 개로 나누지 않고 하나의 함수로 쓰면

def check(y, x, check_num):
    BOX_SIZE = 3
    
    for i in range(SIZE): # 가로, 세로 체크
        if sudoku[y][i] == check_num or sudoku[i][x] == check_num:
            return False
    
    for i in range(BOX_SIZE): # 3x3영역 체크
        for j in range(BOX_SIZE):
            if sudoku[y // BOX_SIZE * BOX_SIZE + i][x // BOX_SIZE * BOX_SIZE + j] == check_num:
                return False
    return True

이렇게 check 함수를 만들 수 있다.

3. DFS

그리고 탐색을 진행한다.

위에서 빈칸과 스도쿠 판 모두 [y, x] 좌표의 형태를 가진다고 했으므로

def dfs(n):      
    for check_num in range(1,10):
        y, x = blank_coord[n]
        # y = blank_coord[n][0]
        # x = blank_coord[n][1]
        
        if check(y, x, check_num):
            sudoku[y][x] = check_num
            dfs(n+1)
            sudoku[y][x] = 0

로 DFS를 구현하고,

가능한 답이 나오면 종료하고 반환하는 것까지 추가해준다.

if n == len(blank_coord):
    for i in sudoku: 
        print(*i) 
    exit()

전체 풀이 코드

import sys

SIZE = 9

sudoku = [list(map(int,sys.stdin.readline().split())) for _ in range(SIZE)] # 스도쿠 문제
blank_coord = [(i, j) for i in range(SIZE) for j in range(SIZE) if sudoku[i][j] == 0] # 빈칸의 좌표를 나타낸 리스트

def check(y, x, check_num):
    BOX_SIZE = 3
    
    for i in range(SIZE): # 가로, 세로 체크
        if sudoku[y][i] == check_num or sudoku[i][x] == check_num:
            return False
    
    for i in range(BOX_SIZE): # 3x3영역 체크
        for j in range(BOX_SIZE):
            if sudoku[y // BOX_SIZE * BOX_SIZE + i][x // BOX_SIZE * BOX_SIZE + j] == check_num:
                return False
    return True

def dfs(n):
    if n == len(blank_coord):
        for i in sudoku: 
            print(*i) 
        exit() 
    
    for check_num in range(1,10):
        y, x = blank_coord[n]
        # y = blank_coord[n][0]
        # x = blank_coord[n][1]
        if check(y, x, check_num):
            sudoku[y][x] = check_num
            dfs(n+1)
            sudoku[y][x] = 0
            
dfs(0)

두 번째 방법

풀이과정

1. 초기조건

위 첫 번째 방법과 마찬가지로 전체 스도쿠 판과 빈칸에 대한 리스트를 만든다. (자세한 설명은 위에 있으니 패스)

다른 점은, 모든 칸의 합을 구해야 한다는 것.

또한 종료 조건에 빈칸의 갯수가 필요하지 않으므로 빈 칸 좌표를 저장한 리스트도 필요없다.

SIZE = 9

# 스도쿠 문제
sudoku = [list(map(int,sys.stdin.readline().split())) for _ in range(SIZE)] 

# 모든 칸의 합
total_sum = sum(map(sum, sudoku))

2. 각 조건 체크

이 역시 위의 첫 번째 방법과 동일

def check(y, x, check_num):
    BOX_SIZE = 3
    
    for i in range(SIZE): # 가로, 세로 체크
        if sudoku[y][i] == check_num or sudoku[i][x] == check_num:
            return False
    
    for i in range(BOX_SIZE): # 3x3영역 체크
        for j in range(BOX_SIZE):
            if sudoku[y // BOX_SIZE * BOX_SIZE + i][x // BOX_SIZE * BOX_SIZE + j] == check_num:
                return False
    return True

3. DFS

종료 조건만 모든 빈칸 갯수만큼 DFS → 합이 405인 경우로 바꿔준다.

이 때는 다음 DFS에서 합이 405가 되는지도 확인해야 하기 때문에, 함수에 합을 같이 넣어준다.

def dfs(n, current_sum):
    global total_sum

    if total_sum == 405:
        # 총 합이 405이면 종료
        for x in sudoku:
            print(*x)
        return True

그리고 각 칸에 대해 탐색을 진행하고, 0일때만 탐색하도록 한다.

DFS에 들어가는 인덱스는 일차원이므로, 이차원으로 바꿔준 후에 진행한다.

    # 일차원 리스트 인덱스를 이차원 좌표로 변환
    y = n // SIZE # y좌표
    x = n % SIZE # x좌표
    
    # 해당 칸의 숫자가 0이라면 탐색 
    if sudoku[y][x] == 0:
    
        for check_num in range(1, 10):  # 조건에 맞다면 숫자를 채우고 합함
            if check(y, x, check_num):
                sudoku[y][x] = check_num
                total_sum += check_num
                
                # 재귀 : 다음 위치로 이동, dfs 진행
                if dfs(n + 1, current_sum + check_num):
                    return True
                '''
                실패하면 - dfs(n+1)에서 1~9까지 다 넣어도 통과하지 못한다
                dfs(n)에 넣은 수가 잘못된 것이므로 다른 숫자로 시도해보기 위해 원래 상태로 되돌림
                '''
                sudoku[y][x] = 0
                total_sum -= check_num
                
    else: # 0이 아니라면 다음 위치로 이동
        return dfs(n + 1, current_sum)

전체 풀이 코드

import sys

SIZE = 9

sudoku = [list(map(int,sys.stdin.readline().split())) for _ in range(SIZE)]
    # 스도쿠 퍼즐의 모든 셀의 합 초기화
total_sum = sum(map(sum, sudoku))

def check(y, x, check_num):
    BOX_SIZE = 3
    
    for i in range(SIZE): # 가로, 세로 체크
        if sudoku[y][i] == check_num or sudoku[i][x] == check_num:
            return False
    
    for i in range(BOX_SIZE): # 3x3영역 체크
        for j in range(BOX_SIZE):
            if sudoku[y // BOX_SIZE * BOX_SIZE + i][x // BOX_SIZE * BOX_SIZE + j] == check_num:
                return False
    return True

def dfs(n, current_sum):
    global total_sum

    if total_sum == 405:
        # 총 합이 405이면 종료
        for x in sudoku:
            print(*x)
        return True

    # 일차원 리스트 인덱스를 이차원 좌표로 변환
    y = n // SIZE # y좌표
    x = n % SIZE # x좌표

    # 해당 칸의 숫자가 0이라면 탐색 
    if sudoku[y][x] == 0:
        for check_num in range(1, 10):
            
            if check(y, x, check_num): # 조건에 맞다면 숫자를 채우고 합함
                sudoku[y][x] = check_num
                total_sum += check_num
                
                if dfs(n + 1, current_sum + check_num):  # 재귀 : 다음 위치로 이동
                    return True
                '''
                실패하면 - dfs(n+1)에서 1~9까지 다 넣어도 통과하지 못한다
                dfs(n)에 넣은 수가 잘못된 것이므로 다른 숫자로 시도해보기 위해 원래 상태로 되돌림
                '''
                sudoku[y][x] = 0
                total_sum -= check_num
                
    else: # 0이 아니라면 다음 위치로 이동
        return dfs(n + 1, current_sum)

dfs(0, 0)

시간은 엇비슷하긴 하지만 여러번 해봤을 때 평균적으로 2번 방법이 살짝 더 빨랐다.